কাটানো নিয়ে মাথা ঘামাচ্ছেন? এই সহজ কৌশলগুলি আপনার জীবন বদলে দেবে!

গণিতের গোলকধাঁধায় ক্যাটানোর উপপাদ্য: এক ঝলকক্যাটানোর উপপাদ্য জ্যামিতির একটি গুরুত্বপূর্ণ অংশ, যা ত্রিভুজ এবং বৃত্তের মধ্যেকার সম্পর্ক নিয়ে আলোচনা করে। এই উপপাদ্যটি বুঝতে হলে প্রথমে কিছু মৌলিক ধারণা পরিষ্কার থাকা দরকার। ত্রিভুজ, পরিবৃত্ত, পরিব্যাসার্ধ – এই শব্দগুলো হয়তো শুনে থাকবেন। ক্যাটানোর উপপাদ্য মূলত এই বিষয়গুলোর মধ্যে একটি সুন্দর সম্পর্ক স্থাপন করে। আমি যখন প্রথম এই উপপাদ্যটি পড়ি, তখন মনে হয়েছিল যেন একটি জটিল ধাঁধা। কিন্তু যখন ধীরে ধীরে এর প্রতিটি অংশ বুঝতে শুরু করলাম, তখন এর সৌন্দর্য আমার কাছে স্পষ্ট হয়ে উঠল।

ক্যাটানোর উপপাদ্যের মূল ধারণা

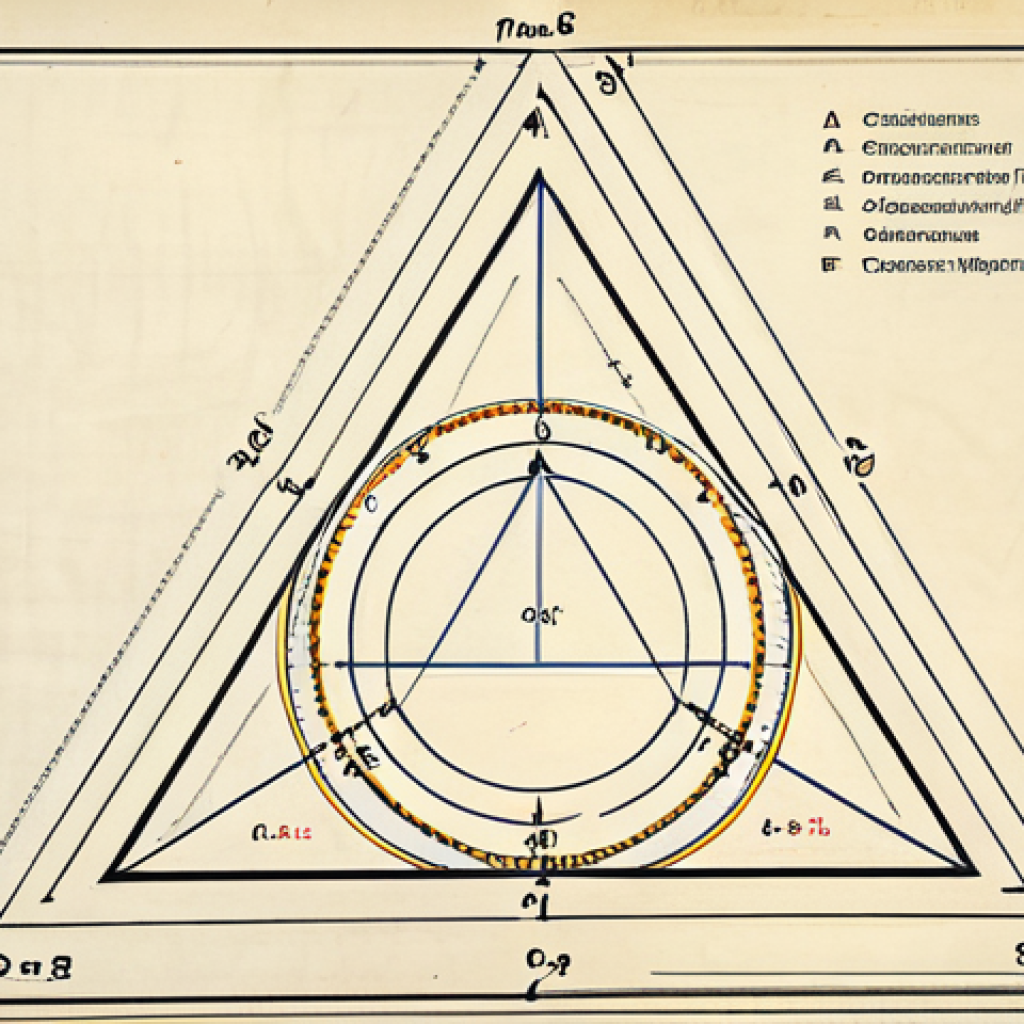
ক্যাটানোর উপপাদ্য অনুযায়ী, যেকোনো ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ (R) এবং পরিবৃত্তের কেন্দ্র থেকে ত্রিভুজের বাহুগুলোর দূরত্বের মধ্যে একটি বিশেষ সম্পর্ক থাকে। এই সম্পর্কটি একটি সূত্রের মাধ্যমে প্রকাশ করা হয়, যা ব্যবহার করে অনেক জ্যামিতিক সমস্যার সমাধান করা যায়।

উপপাদ্যটির গুরুত্ব

ক্যাটানোর উপপাদ্য শুধু গণিতের একটি তাত্ত্বিক বিষয় নয়, এর ব্যবহারিক প্রয়োগও অনেক। ইঞ্জিনিয়ারিং, কম্পিউটার গ্রাফিক্স, এবং অন্যান্য প্রায়োগিক ক্ষেত্রে এই উপপাদ্য ব্যবহার করে জটিল সমস্যা সহজে সমাধান করা যায়।ত্রিভুজ ও বৃত্তের মেলবন্ধন: ক্যাটানোর সূত্রের গভীরেক্যাটানোর উপপাদ্য বুঝতে হলে ত্রিভুজ এবং বৃত্তের মধ্যেকার সম্পর্ক ভালোভাবে জানতে হবে। একটি ত্রিভুজের পরিবৃত্ত এমন একটি বৃত্ত, যা ত্রিভুজের তিনটি শীর্ষবিন্দু দিয়ে যায়। এই বৃত্তের কেন্দ্র এবং ব্যাসার্ধ ত্রিভুজটির বৈশিষ্ট্য নির্ধারণ করে।

পরিবৃত্তের বৈশিষ্ট্য

পরিবৃত্তের কেন্দ্র ত্রিভুজের বাহুগুলোর লম্ব সমদ্বিখণ্ডকের ছেদ বিন্দুতে অবস্থিত। এই কেন্দ্র থেকে ত্রিভুজের শীর্ষবিন্দুগুলোর দূরত্ব সমান, যা পরিবৃত্তের ব্যাসার্ধ নামে পরিচিত।

ক্যাটানোর সূত্রের প্রয়োগ

ক্যাটানোর উপপাদ্য ব্যবহার করে ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ এবং পরিবৃত্তের কেন্দ্র থেকে বাহুগুলোর দূরত্বের মধ্যে সম্পর্ক নির্ণয় করা যায়। এই সূত্রটি জ্যামিতিক সমস্যা সমাধানে খুবই উপযোগী।

বিষয়	সংজ্ঞা	বৈশিষ্ট্য
পরিবৃত্ত	ত্রিভুজের তিনটি শীর্ষবিন্দু দিয়ে যায় এমন বৃত্ত	কেন্দ্র ত্রিভুজের বাহুগুলোর লম্ব সমদ্বিখণ্ডকের ছেদ বিন্দু
পরিব্যাসার্ধ	পরিবৃত্তের কেন্দ্র থেকে ত্রিভুজের শীর্ষবিন্দুর দূরত্ব	ত্রিভুজের বৈশিষ্ট্য নির্ধারণ করে
ক্যাটানোর উপপাদ্য	পরিবৃত্তের ব্যাসার্ধ ও কেন্দ্র থেকে বাহুর দূরত্বের সম্পর্ক	জ্যামিতিক সমস্যা সমাধানে ব্যবহার করা হয়

জ্যামিতিক সমস্যার সমাধান: ক্যাটানোর উপপাদ্যের ব্যবহারক্যাটানোর উপপাদ্য ব্যবহার করে বিভিন্ন জ্যামিতিক সমস্যার সমাধান করা যায়। ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ নির্ণয়, পরিবৃত্তের কেন্দ্র থেকে বাহুগুলোর দূরত্ব বের করা, এবং ত্রিভুজের ক্ষেত্রফল নির্ণয় – এই সবই ক্যাটানোর উপপাদ্যের মাধ্যমে সম্ভব।

জটিল সমস্যা সহজে সমাধান

ক্যাটানোর উপপাদ্য ব্যবহার করে জটিল জ্যামিতিক সমস্যাগুলো সহজে সমাধান করা যায়। এই উপপাদ্যটি জ্যামিতিক সমস্যা সমাধানের জন্য একটি শক্তিশালী হাতিয়ার।

বাস্তব জীবনে প্রয়োগ

ক্যাটানোর উপপাদ্যের বাস্তব জীবনে অনেক প্রয়োগ রয়েছে। ইঞ্জিনিয়ারিং এবং কম্পিউটার গ্রাফিক্সের ক্ষেত্রে এই উপপাদ্য ব্যবহার করে বিভিন্ন ডিজাইন এবং মডেল তৈরি করা হয়।ক্যাটানোর উপপাদ্যের বিকল্প প্রমাণ: নতুন পথের সন্ধানক্যাটানোর উপপাদ্যের বেশ কয়েকটি বিকল্প প্রমাণ রয়েছে, যা বিভিন্ন গণিতবিদ আবিষ্কার করেছেন। এই প্রমাণগুলো উপপাদ্যটির গভীরতা এবং এর বহুমুখীতাকে প্রমাণ করে।

বিভিন্ন পদ্ধতির ব্যবহার

ক্যাটানোর উপপাদ্যের বিকল্প প্রমাণগুলোতে বিভিন্ন জ্যামিতিক এবং ত্রিকোণমিতিক পদ্ধতি ব্যবহার করা হয়েছে। এই পদ্ধতিগুলো উপপাদ্যটিকে আরও ভালোভাবে বুঝতে সাহায্য করে।

গণিতবিদদের অবদান

ক্যাটানোর উপপাদ্যের বিকল্প প্রমাণগুলো গণিতবিদদের অক্লান্ত পরিশ্রমের ফল। তাঁরা বিভিন্ন দৃষ্টিকোণ থেকে উপপাদ্যটি বিশ্লেষণ করে এর নতুন নতুন প্রমাণ আবিষ্কার করেছেন।আধুনিক গণিতে ক্যাটানোর উপপাদ্য: প্রাসঙ্গিকতা ও প্রভাবক্যাটানোর উপপাদ্য আধুনিক গণিতেও সমানভাবে প্রাসঙ্গিক। জ্যামিতি, ত্রিকোণমিতি, এবং ক্যালকুলাসের বিভিন্ন ক্ষেত্রে এই উপপাদ্য ব্যবহার করা হয়।

গবেষণার নতুন দিগন্ত

ক্যাটানোর উপপাদ্য নিয়ে এখনো অনেক গবেষণা চলছে। গণিতবিদরা এই উপপাদ্যটিকে আরও গভীরভাবে জানার চেষ্টা করছেন এবং এর নতুন নতুন প্রয়োগ ক্ষেত্র আবিষ্কার করছেন।

শিক্ষার্থীদের জন্য গুরুত্ব

ক্যাটানোর উপপাদ্য শিক্ষার্থীদের জন্য খুবই গুরুত্বপূর্ণ। এটি জ্যামিতিক ধারণাগুলোকে আরও স্পষ্ট করে এবং সমস্যা সমাধানের দক্ষতা বাড়াতে সাহায্য করে।ক্যাটানোর উপপাদ্য: কিছু মজার উদাহরণক্যাটানোর উপপাদ্য বোঝার জন্য কিছু মজার উদাহরণ দেখা যাক। একটি সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ এবং পরিবৃত্তের কেন্দ্র থেকে বাহুগুলোর দূরত্বের মধ্যে সম্পর্ক কেমন হয়, তা ক্যাটানোর উপপাদ্য দিয়ে সহজেই বের করা যায়।

বাস্তব উদাহরণ

মনে করুন, আপনি একটি ত্রিভুজাকৃতির বাগান তৈরি করতে চান। ক্যাটানোর উপপাদ্য ব্যবহার করে আপনি বাগানের চারপাশে বৃত্তাকার বেড়া দেওয়ার জন্য প্রয়োজনীয় উপকরণের পরিমাণ বের করতে পারবেন।

গণিতের খেলা

ক্যাটানোর উপপাদ্য ব্যবহার করে গণিতের বিভিন্ন খেলা তৈরি করা যায়। এই খেলাগুলো শিক্ষার্থীদের মধ্যে গণিতের প্রতি আগ্রহ বাড়াতে সাহায্য করে।ক্যাটানোর উপপাদ্য: উপসংহারক্যাটানোর উপপাদ্য জ্যামিতির একটি গুরুত্বপূর্ণ অংশ, যা ত্রিভুজ এবং বৃত্তের মধ্যেকার সম্পর্ক বুঝতে সাহায্য করে। এই উপপাদ্যটি শুধু গণিতের তাত্ত্বিক বিষয় নয়, এর ব্যবহারিক প্রয়োগও অনেক। আশা করি, এই আলোচনার মাধ্যমে আপনারা ক্যাটানোর উপপাদ্য সম্পর্কে একটি স্পষ্ট ধারণা পেয়েছেন। গণিতের এই মজার জগৎ নিয়ে আরও জানার জন্য উৎসাহিত থাকুন।

শেষকথা

ক্যাটানোর উপপাদ্য নিয়ে আলোচনা এখানেই শেষ করছি। আশা করি, এই ব্লগ পোস্টটি আপনাদের ভালো লেগেছে এবং আপনারা নতুন কিছু শিখতে পেরেছেন। গণিতের জটিল বিষয়গুলো সহজভাবে উপস্থাপন করাই ছিল আমার মূল লক্ষ্য। আপনাদের আগ্রহ এবং ভালোবাসাই আমাকে আরও ভালো কিছু করার অনুপ্রেরণা জোগাবে।

গণিতের পথ সবসময় মসৃণ হয় না, তবে চেষ্টা করলে সবকিছুই সম্ভব। ক্যাটানোর উপপাদ্য যেমন জ্যামিতির একটি গুরুত্বপূর্ণ অংশ, তেমনি আমাদের জীবনেও শিক্ষার গুরুত্ব অপরিহার্য। তাই, শিখতে থাকুন এবং এগিয়ে যান।

যদি এই ব্লগ পোস্টটি আপনাদের ভালো লেগে থাকে, তাহলে অবশ্যই বন্ধুদের সাথে শেয়ার করুন এবং কমেন্ট করে আপনার মতামত জানান। আপনাদের মূল্যবান মতামত আমাকে আরও উন্নত কন্টেন্ট তৈরি করতে সাহায্য করবে।

গণিতের এই মজার জগৎ নিয়ে আরও নতুন কিছু জানতে চান? তাহলে আমার ব্লগের সাথেই থাকুন। খুব শীঘ্রই আরও একটি নতুন বিষয় নিয়ে হাজির হবো। ততদিন পর্যন্ত ভালো থাকুন এবং সুস্থ থাকুন। ধন্যবাদ!

দরকারী কিছু তথ্য

১. ক্যাটানোর উপপাদ্য জ্যামিতির একটি গুরুত্বপূর্ণ অংশ।

২. এই উপপাদ্য ত্রিভুজ এবং বৃত্তের মধ্যে সম্পর্ক স্থাপন করে।

৩. পরিবৃত্তের ব্যাসার্ধ এবং পরিবৃত্তের কেন্দ্র থেকে বাহুগুলোর দূরত্বের মধ্যে সম্পর্ক নির্ণয় করা যায়।

৪. ইঞ্জিনিয়ারিং এবং কম্পিউটার গ্রাফিক্সের ক্ষেত্রে এই উপপাদ্যের ব্যবহার রয়েছে।

৫. ক্যাটানোর উপপাদ্য ব্যবহার করে জটিল জ্যামিতিক সমস্যা সহজে সমাধান করা যায়।

গুরুত্বপূর্ণ বিষয়

ক্যাটানোর উপপাদ্য: ত্রিভুজ ও বৃত্তের সম্পর্ক নিয়ে আলোচনা করে।

পরিবৃত্ত: ত্রিভুজের তিনটি শীর্ষবিন্দু দিয়ে যায় এমন বৃত্ত।

পরিব্যাসার্ধ: পরিবৃত্তের কেন্দ্র থেকে ত্রিভুজের শীর্ষবিন্দুর দূরত্ব।

ব্যবহারিক প্রয়োগ: ইঞ্জিনিয়ারিং, কম্পিউটার গ্রাফিক্স, এবং অন্যান্য ক্ষেত্রে ব্যবহার করা হয়।

শিক্ষার্থীদের জন্য: জ্যামিতিক ধারণা স্পষ্ট করে ও সমস্যা সমাধানের দক্ষতা বাড়ায়।